Diffusion Model (DDPM)

참고 블로그 : 링크
배경지식 : VAE
원본 논문 : 논문

Pasted image 20250317143658.png

논문의 의의

논문은 매우 복잡하지만 내가 파악한 의의는
기존의 DM에서의 Log-likelihood 형태의 Loss를 MSE 기반의 Loss 형태로 표현해 학습을 쉽게 함!
이다.

Diffusion Model의 기본 구조

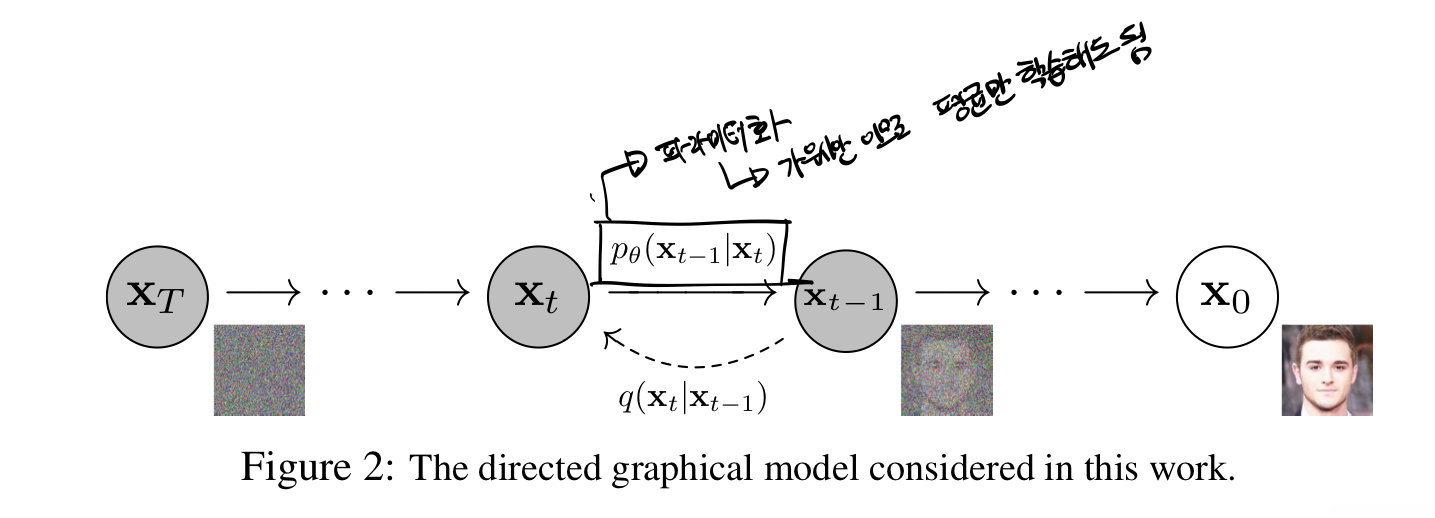
Forward Process

원본 데이터 X0에서 가우시안 노이즈를 조금씩 조금씩 추가해서 최종적으로 완전히 가우시안 노이즈가 된 xT를 만듬. (T만큼의 step만큼 노이즈를 추가)
이 때 각 과정은 Markov Process로 진행되기에, 각 step은 그 이전의 이미지 상태에만 영향을 받고, 노이즈 추가를 q(xt|xt−1)으로 표현할 수 있다.

Reverse Process

디퓨전 모델은 가우시안 노이즈 XT에서 원본 데이터 X0를 생성하기 위함이다.
이 과정에서 각 step은 파라미터화 되어 있어, 딥러닝 모델을 통해 복원을 수행한다.
이 역시 마르코프 프로세스이다.
각 step을 pθ(xt−1|xt)라고 할 수 있다.
이 때, denoising 단계는 gaussian이기 때문에 딥러닝 모델은 평균만 학습해도 그만이다.
이 process의 목적은 역시나 기존 이미지와의 Likelihood를 최대화 하는 것이다.

VAE와의 관계?

여기서 순차적으로 노이즈를 추가하고 순차적으로 denoise 하지 않고, 한번에 해버리면 VAE가 된다.

Denoising Diffusion Probabilistic Model

이 논문의 목적

이 논문 이전에는 디퓨젼 모델이라는 개념 자체는 제안되었지만, 그 훈련의 과정 및 결과물이 만족스럽지 않았다 (고품질의 이미지를 생성하지 못함)
이 논문에서는 아래와 같은 기여들을 했는데, 도대체 이 기여들이 무엇일까를 알아보는 것이 이번 논문의 도전 되시겠다.

  1. Diffusion Probabilistic Model과 Denoising score matching간의 novel한 관계가 있다.
    1. 아래 설명을 보다 보면 Lsimple과 같은 loss 값이 MSE의 형태를 띄게 된다. 이렇게 단순화된 loss는 사실상 Denoising score matching, 즉 denoise autoencoder에서 노이즈가 얼마나 지워졌는지 단순하게 판단하는 방식과 매우 유사하다는 것이다.
  2. progressive lossy decompression scheme을 포함한다.
    => "progressive" 각 step 별로 decompression을 하려는 모델이 포함되며, loss도 이 decompression을 잘하기 위하도록 훈련된다.
  3. Diffusion model의 샘플링은 ARM (Auto Regressive Model)의 디코딩과 유사하다.
    => 아무래도 단계별로 분포를 예측하는 것이니깐 유사하다고 볼 수 있다?
    (뭔소리야????)
    뭔소리인지 모르겠으니 알아보자

Forward Process

q(Xt|Xt−1)=N(Xt;1−βtXt−1,βtI)=1−βtXt−1+βtϵt−1

여기서 ϵ N(0,1)입니다. (Reparameterization Trick)
βtI만큼 가우시안 노이즈를 더해가는 것으로 생각할 수 있습니다.

α¯t:=∏s=1t(1−βs) 이라면 아래와 같이도 표현할 수 있습니다.

q(Xt|X0)=N(Xt;α¯tX0,(1−α¯t)I)=α¯tX0+1−α¯tϵt−1

Reverse Process

Forward process에서 가우시안 분포로 noise를 주었는데, 그 역방향 분포도 가우시안 분포라는 것이 이미 증명됨. (받아드리셈 ㅇㅇ)

그래서 p(XT)=N(XT;0,I)일 때, 다음과 같이 표현할 수 있음.

pθ(X0:T):=p(XT)∏t=1Tpθ(Xt−1|Xt)pθ(Xt−1|Xt):=N(Xt−1;μθ(Xt,t),Σθ(Xt,t))

여기서 θ가 붙은 것들은 죄다 파라미터화, 즉 딥러닝 모델이라고 생각하면 됨.
즉 각 step마다 딥러닝 모델을 활용해 어떤 가우시안 distribution으로 denoise를 할지 평균과 분산을 예측하는 것.

Loss Function

Pasted image 20250317164913.png
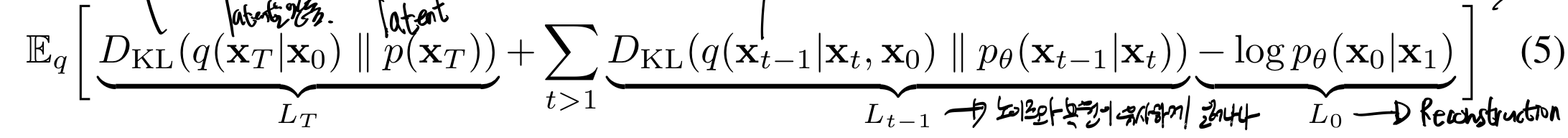
Pasted image 20250317213101.png

pθ(X0)을 최대화하도록, 즉 negative log likelihood를 최소화하는 방식으로 학습을 진행할 것이다.
이것을 어떻게 어떻게 전개하면 아래처럼 세 process로 나누어진 loss가 된다.

1. Regularization Error

DKL(q(XT|X0)||p(XT))

여기서 p(XT) (완전 가우시안 노이즈)랑 q(XT|X0), 즉 Forward process를 거친 후에 노이즈는 사실상 완전 가우시안 노이즈다.
그니깐 KL term이 사실상 제로가 된다.
그래서 계산할 필요 없음.

논문에서는 살짝 다르게 설명하는데, βt (가우시안 노이즈를 얼마나 줄 것인지 결정하는 파라미터)가 학습이 되지 않는 상수로 진행하기로 했기 때문에, 역시 Regularization Error도 하나의 상수로 결정될 수 있다고 한다. 맞는 소리다. (그리고 역시나 사실상 제로가 되겠지)

2. Denoising Error

DKL(q(Xt−1|Xt,X0)||pθ(Xt−1|Xt))

여기서 DKL(q(Xt−1|Xt,X0))은 계산이 쉽다고 한다... (왜? 몰라 찾아보세유)
이 정규분포를 알 수 있으니깐, pθ(Xt−1|Xt) 학습이 가능하다.

이러쿵저러쿵.... 증명을 하면 아래와 같이 Denoising Error는 계산 가능하다.

EX0,ϵ[βt22σt2αt(1−α¯t)||ϵ−ϵθ(α¯tX0+1−α¯tϵ,t)||2]

βt와 α¯t, 그리고 αt는 학습 전부터 미리 정해져 있고, 대충 ϵθ만 계산하면 (모델의 결과) loss를 구할 수 있다.

갑자기 결론

그래서 아래처럼 simplified 해서 표현할 수 있다.

L_{simple}(\theta) := \mathbb{E}_{t, X_0, \epsilon}[|| \epsilon - \epsilon_\theta(\sqrt{\bar \alpha_t}X_0 + \sqrt{1-\bar \alpha_t} \epsilon, t) || { #2} ]

그래서 쉽게 학습이 가능하다고 한다 (MSE 같으시잖아 한잔해)

훈련 및 인퍼런스

Pasted image 20250408172324.png

DDPM Train 과정

  1. 데이터셋에서 데이터를 샘플링한다.
  2. 1~T 중에 특정 step을 랜덤으로 고른다. (노이즈 스케줄이 정해져있기 때문에 순차적이 아닌 마구잡이로 학습할 수 있다)
  3. N(0,I)를 따르는 노이즈를 샘플링한다.
  4. 이제 Lsimple을 계산하고 그 그라디언트를 이용해 모델 ϵθ를 업데이트한다.

DDPM 인퍼런스 과정

  1. 생성을 시작할 노이즈를 N(0,I)에서 샘플링한다.
  2. 이제 T부터 순차적으로 모델 ϵθ를 이용해서 디노이즈 한다.
  3. 마지막으로 생성 결과 X0를 리턴한다.

(추가 논의) Diffusion Model은 Image의 Inductive Bias에 어떻게 효율적인가

Latent Diffusion Model (LDM) 논문 중 아래와 같은 내용이 나옴.

Since diffusion models offer excellent inductive biases for spatial data

viT 논문에서 나왔던 image의 inductive bias는 다음과 같다.

  1. Locality
  2. translation equivariance
  3. two-dimensional neighborhood structure

이유

대체로 Denoiser를 CNN 기반으로 사용한다 (e.g. U-Net)
그래서 inductive bias에 fit함
(Latent Diffusion Model (LDM) 마지막 부분 참고하기)

왜 reweighted objective?

βt는 시간이 지날수록 증가한다. 즉, diffusion process step에 따라서 노이즈를 얼마나 주는 지가 달라진다.

L_{simple}(\theta) := \mathbb{E}_{t, X_0, \epsilon}[|| \epsilon - \epsilon_\theta(\sqrt{\bar \alpha_t}X_0 + \sqrt{1-\bar \alpha_t} \epsilon, t) || { #2} ]

마지막 loss를 보면 α¯t안에 βt가 포함되어 있다는 것을 기억해 보자. 이 βt가 시간에 따라 달라지기 때문에, loss 자체에 weight가 각 step 별로 달라진다고 볼 수도 있다.

왜 Lossy compressor?